中２数学 発展問題 解答プリント 一次関数４ 式の求め方 画像

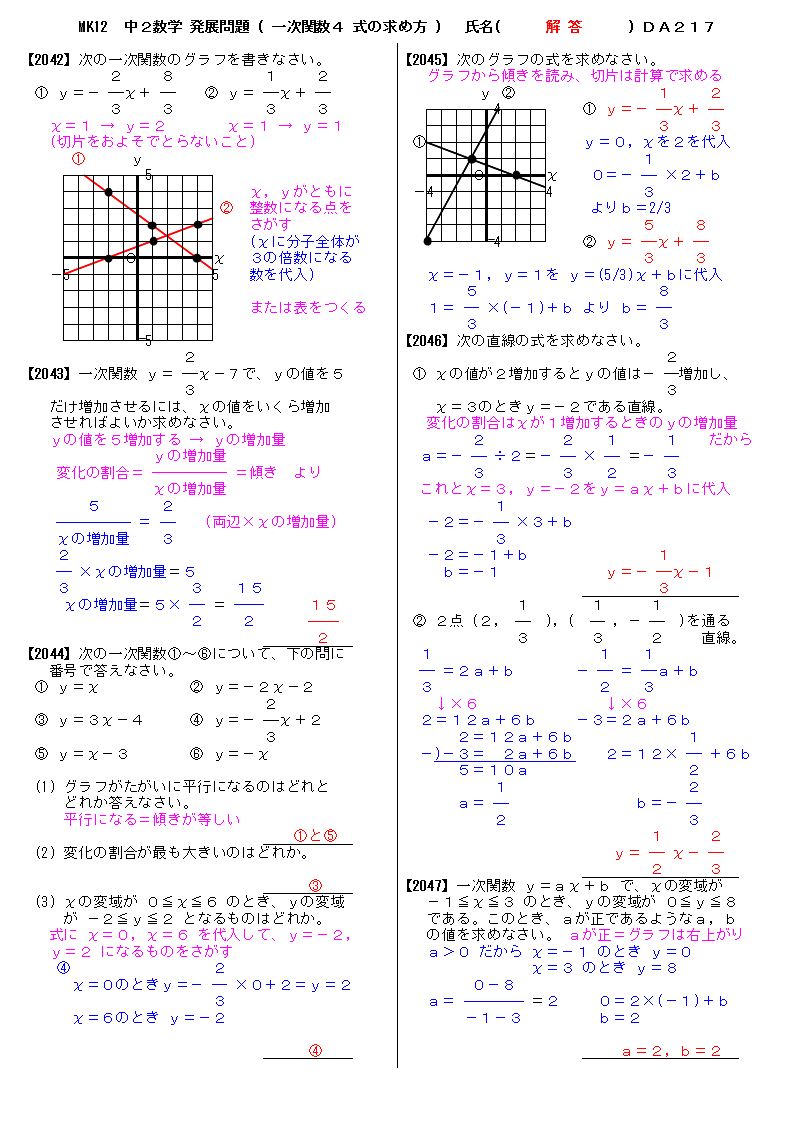
中２数学 発展問題 解答プリント 一次関数４ 式の求め方 テキスト

マスコン 中２数学 発展問題 ( 一次関数４ 式の求め方 ) 氏名( 解 答 ) ＤＡ２１７ 【2042】次の一次関数のグラフを書きなさい。 【2045】次のグラフの式を求めなさい。 ２ ８ １ ２ グラフから傾きを読み、切片は計算で求める �@ ｙ＝− χ＋ �A ｙ＝ χ＋ ｙ �A １ ２ ３ ３ ３ ３ 4 �@ ｙ＝− χ＋ χ＝１ → ｙ＝２ χ＝１ → ｙ＝１ ３ ３ (切片をおよそでとらないこと) �@ ｙ＝０，χを２を代入 �@ ｙ １ 5 ０ χ ０＝− ×２＋ｂ χ，ｙがともに −4 4 ３ �A 整数になる点を よりｂ＝2/3 さがす ５ ８ (χに分子全体が 4 �A ｙ＝ χ＋ ０ χ ３の倍数になる ３ ３ −5 5 数を代入) χ＝−１，ｙ＝１を ｙ＝(5/3)χ＋ｂに代入 ５ ８ または表をつくる １＝ ×(−１)＋ｂ より ｂ＝ ３ ３ 5 【2046】次の直線の式を求めなさい。 ２ ２ 【2043】一次関数 ｙ＝ χ−７で、ｙの値を５ �@ χの値が２増加するとｙの値は− 増加し、 ３ ３ だけ増加させるには、χの値をいくら増加 χ＝３のときｙ＝−２である直線。 させればよいか求めなさい。 変化の割合はχが１増加するときのｙの増加量 ｙの値を５増加する → ｙの増加量 ２ ２ １ １ だから ｙの増加量 ａ＝− ÷２＝− × ＝− 変化の割合＝ ＝傾き より ３ ３ ２ ３ χの増加量 これとχ＝３，ｙ＝−２をｙ＝ａχ＋ｂに代入 ５ ２ １ ＝ (両辺×χの増加量) −２＝− ×３＋ｂ χの増加量 ３ ３ ２ −２＝−１＋ｂ １ ×χの増加量＝５ ｂ＝−１ ｙ＝− χ−１ ３ ３ １５ ３ χの増加量＝５× ＝ １５ １ １ １ ２ ２ �A ２点 (２， )，( ，− )を通る ２ ３ ３ ２ 直線。 【2044】次の一次関数�@〜�Eについて、下の問に １ １ １ 番号で答えなさい。 ＝２ａ＋ｂ − ＝ ａ＋ｂ �@ ｙ＝χ �A ｙ＝−２χ−２ ３ ２ ３ ２ ↓×６ ↓×６ �B ｙ＝３χ−４ �C ｙ＝− χ＋２ ２＝１２ａ＋６ｂ −３＝２ａ＋６ｂ ３ ２＝１２ａ＋６ｂ １ �D ｙ＝χ−３ �E ｙ＝−χ −)−３＝ ２ａ＋６ｂ ２＝１２× ＋６ｂ ５＝１０ａ ２ (1) グラフがたがいに平行になるのはどれと １ ２ どれか答えなさい。 ａ＝ ｂ＝− 平行になる＝傾きが等しい ２ ３ �@と�D １ ２ (2) 変化の割合が最も大きいのはどれか。 ｙ＝ χ− ２ ３ �B 【2047】一次関数 ｙ＝ａχ＋ｂ で、χの変域が (3) χの変域が ０≦χ≦６ のとき、ｙの変域 −１≦χ≦３ のとき、ｙの変域が ０≦ｙ≦８ が −２≦ｙ≦２ となるものはどれか。 である。このとき、ａが正であるようなａ，ｂ 式に χ＝０，χ＝６ を代入して、ｙ＝−２， の値を求めなさい。 ａが正＝グラフは右上がり ｙ＝２ になるものをさがす ａ＞０ だから χ＝−１ のとき ｙ＝０ �C ２ χ＝３ のとき ｙ＝８ χ＝０のときｙ＝− ×０＋２＝ｙ＝２ ０−８ ３ ａ＝ ＝２ ０＝２×(−１)＋ｂ χ＝６のとき ｙ＝−２ −１−３ ｂ＝２ �C ａ＝２，ｂ＝２

中２数学の学習プリントのＰＤＦファイル

中２数学の学習プリントはＰＤＦファイルで項目別にまとめてダウンロードできます。
全て、問題プリントと解答プリントのセットです。（ヒントページはありません）

中２数学の学習プリントのＰＤＦファイルダウンロードリンク（有料）

中２数学の解説と確認問題セット　数学の苦手な生徒向きです。

中２数学の基本問題集セット　きっちりやればテストで平均点くらいは取れます。

中２数学の標準問題集セット　テストで平均点以上を目指す生徒向きです。

中２数学の発展問題集セット　学年上位やハイレベルの高校を目指す生徒向きです。

中２数学のテスト対策問題集セット　テスト前にやると効果的です。

中２数学の問題集fullset(総合版)　解説・基本・標準・発展・テストの５種類のプリントをセットにしてあるものです。

■各学年の総合版は、こちらから銀行振込でも購入できます。

中学２年数学の参考書・問題集

中２数学の教科書ガイド
中２数学の問題集
中２数学の解説ＤＶＤ
中２数学の教科書ガイド（楽天）

お勧め情報