無料 中２数学 基本解説 解答プリント 式の計算４ いろいろな計算 画像

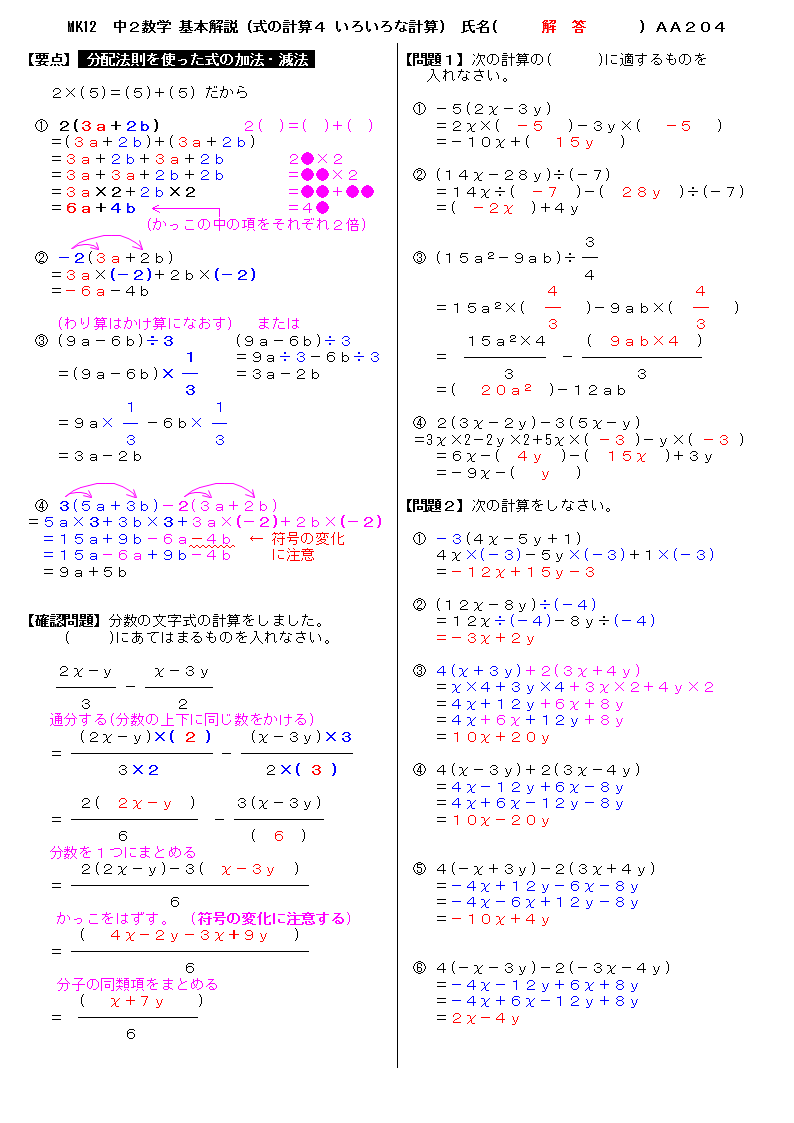
無料 中２数学 基本解説 解答プリント 式の計算４ いろいろな計算 テキスト

マスコン 中２数学 基本解説 (式の計算４ いろいろな計算) 氏名( 解 答 ) ＡＡ２０４ 【要点】 分配法則を使った式の加法・減法 【問題１】次の計算の( )に適するものを 入れなさい。 ２×(５)＝(５)＋(５) だから �@ −５(２χ−３ｙ) �@ ２(３ａ＋２ｂ) ２( )＝( )＋( ) ＝２χ×( −５ )−３ｙ×( −５ ) ＝(３ａ＋２ｂ)＋(３ａ＋２ｂ) ＝−１０χ＋( １５ｙ ) ＝３ａ＋２ｂ＋３ａ＋２ｂ ２●×２ ＝３ａ＋３ａ＋２ｂ＋２ｂ ＝●●×２ �A (１４χ−２８ｙ)÷(−７) ＝３ａ×２＋２ｂ×２ ＝●●＋●● ＝１４χ÷( −７ )−( ２８ｙ )÷(−７) ＝６ａ＋４ｂ ＝４● ＝( −２χ )＋４ｙ (かっこの中の項をそれぞれ２倍) ３ �A −２(３ａ＋２ｂ) �B (１５ａ２−９ａｂ)÷ ＝３ａ×(−２)＋２ｂ×(−２) ４ ＝−６ａ−４ｂ ４ ４ ＝１５ａ２×( )−９ａｂ×( ) (わり算はかけ算になおす) または ３ ３ �B (９ａ−６ｂ)÷３ (９ａ−６ｂ)÷３ １５ａ２×４ ( ９ａｂ×４ ) １ ＝９ａ÷３−６ｂ÷３ ＝ − ＝(９ａ−６ｂ)× ＝３ａ−２ｂ ３ ３ ３ ＝( ２０ａ２ )−１２ａｂ １ １ ＝９ａ× −６ｂ× �C ２(３χ−２ｙ)−３(５χ−ｙ) ３ ３ ＝3χ×2−2ｙ×2＋5χ×( −３ )−ｙ×( −３ ) ＝３ａ−２ｂ ＝６χ−( ４ｙ )−( １５χ )＋３ｙ ＝−９χ−( ｙ ) �C ３(５ａ＋３ｂ)−２(３ａ＋２ｂ) 【問題２】次の計算をしなさい。 ＝５ａ×３＋３ｂ×３＋３ａ×(−２)＋２ｂ×(−２) ＝１５ａ＋９ｂ−６ａ−４ｂ ← 符号の変化 �@ −３(４χ−５ｙ＋１) ＝１５ａ−６ａ＋９ｂ−４ｂ に注意 ４χ×(−３)−５ｙ×(−３)＋１×(−３) ＝９ａ＋５ｂ ＝−１２χ＋１５ｙ−３ �A (１２χ−８ｙ)÷(−４) 【確認問題】分数の文字式の計算をしました。 ＝１２χ÷(−４)−８ｙ÷(−４) ( )にあてはまるものを入れなさい。 ＝−３χ＋２ｙ ２χ−ｙ χ−３ｙ �B ４(χ＋３ｙ)＋２(３χ＋４ｙ) − ＝χ×４＋３ｙ×４＋３χ×２＋４ｙ×２ ３ ２ ＝４χ＋１２ｙ＋６χ＋８ｙ 通分する(分数の上下に同じ数をかける) ＝４χ＋６χ＋１２ｙ＋８ｙ (２χ−ｙ)×( ２ ) (χ−３ｙ)×３ ＝１０χ＋２０ｙ ＝ − ３×２ ２×( ３ ) �C ４(χ−３ｙ)＋２(３χ−４ｙ) ＝４χ−１２ｙ＋６χ−８ｙ ２( ２χ−ｙ ) ３(χ−３ｙ) ＝４χ＋６χ−１２ｙ−８ｙ ＝ − ＝１０χ−２０ｙ ６ ( ６ ) 分数を１つにまとめる ２(２χ−ｙ)−３( χ−３ｙ ) �D ４(−χ＋３ｙ)−２(３χ＋４ｙ) ＝ ＝−４χ＋１２ｙ−６χ−８ｙ ６ ＝−４χ−６χ＋１２ｙ−８ｙ かっこをはずす。 (符号の変化に注意する) ＝−１０χ＋４ｙ ( ４χ−２ｙ−３χ＋９ｙ ) ＝ ６ �E ４(−χ−３ｙ)−２(−３χ−４ｙ) 分子の同類項をまとめる ＝−４χ−１２ｙ＋６χ＋８ｙ ( χ＋７ｙ ) ＝−４χ＋６χ−１２ｙ＋８ｙ ＝ ＝２χ−４ｙ ６

中２数学の学習プリントのＰＤＦファイル

中２数学の学習プリントはＰＤＦファイルで項目別にまとめてダウンロードできます。
全て、問題プリントと解答プリントのセットです。（ヒントページはありません）

中２数学の学習プリントのＰＤＦファイルダウンロードリンク（有料）

中２数学の解説と確認問題セット　数学の苦手な生徒向きです。

中２数学の基本問題集セット　きっちりやればテストで平均点くらいは取れます。

中２数学の標準問題集セット　テストで平均点以上を目指す生徒向きです。

中２数学の発展問題集セット　学年上位やハイレベルの高校を目指す生徒向きです。

中２数学のテスト対策問題集セット　テスト前にやると効果的です。

中２数学の問題集fullset(総合版)　解説・基本・標準・発展・テストの５種類のプリントをセットにしてあるものです。

■各学年の総合版は、こちらから銀行振込でも購入できます。

中学２年数学の参考書・問題集

中２数学の教科書ガイド
中２数学の問題集
中２数学の解説ＤＶＤ
中２数学の教科書ガイド（楽天）

お勧め情報